
|
|
| 603 × 57 пикс. Открыть в новом окне | |
и критическая разность для  составит
составит

|
|
| 297 × 57 пикс. Открыть в новом окне | |
4.2.4 Сопоставление с опорным значением более чем для одной лаборатории
Если p лабораториями было получено  результатов измерений со средними арифметическими значениями
результатов измерений со средними арифметическими значениями  (в каждом случае - в условиях повторяемости), общее среднее значение
(в каждом случае - в условиях повторяемости), общее среднее значение 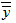 , рассчитывают по формуле
, рассчитывают по формуле
и это общее среднее сравнивают с опорным значением  ; в таком случае стандартное отклонение для
; в таком случае стандартное отклонение для  составит:
составит:
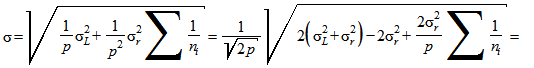
|
|
| 534 × 68 пикс. Открыть в новом окне | |

|
|
| 339 × 68 пикс. Открыть в новом окне | |
и критическая разность для  будет выглядеть следующим образом
будет выглядеть следующим образом

|
|
| 380 × 68 пикс. Открыть в новом окне | |
на уровне вероятности 95%.
4.2.5 Трактовка результатов сопоставления
Если абсолютное расхождение превышает соответствующий предел, приведенный в предыдущих пунктах, то разность должна рассматриваться в качестве подозрительной, и, следовательно, все измерения, которые в результате дали эту разность, должны считаться подозрительными и подлежать дополнительному изучению.
5 Методы проверки приемлемости результатов измерений (испытаний) и установления окончательного результата
5.1 Общие положения
5.1.1 Методы проверки, описанные в настоящем разделе, должны применяться только в том случае, когда измерение выполняют в точном соответствии со стандартным методом измерений, стандартные отклонения которого  и
и 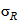 известны. При этом, когда диапазон N результатов измерений превышает соответствующий предел, заданный в разделе 4, считают, что один, два или все N результатов измерений являются отклонениями. Рекомендуется, чтобы причина возникновения отклонений была изучена с технической точки зрения. Тем не менее по соображениям коммерческого характера может оказаться необходимым получение некоторого приемлемого значения и в этих случаях, и тогда с результатами измерений необходимо обращаться в соответствии с положениями настоящего раздела.
известны. При этом, когда диапазон N результатов измерений превышает соответствующий предел, заданный в разделе 4, считают, что один, два или все N результатов измерений являются отклонениями. Рекомендуется, чтобы причина возникновения отклонений была изучена с технической точки зрения. Тем не менее по соображениям коммерческого характера может оказаться необходимым получение некоторого приемлемого значения и в этих случаях, и тогда с результатами измерений необходимо обращаться в соответствии с положениями настоящего раздела.
5.1.2 Настоящий раздел был подготовлен в предположении, что результаты измерений были получены в условиях повторяемости и воспроизводимости, и что доверительный уровень вероятности составляет 95%. Если результаты измерений были получены в промежуточных условиях (см. ГОСТ Р ИСО 5725-3), то  необходимо заменить соответствующей промежуточной мерой.
необходимо заменить соответствующей промежуточной мерой.
5.1.3 В некоторых случаях, там, где процедуры, описываемые в 5.2, приводят к медиане как к конечному результату, более предпочтительным мог бы оказаться отказ от таких данных.
5.2 Методы проверки приемлемости результатов измерений, полученных в условиях повторяемости
Примечание 3 - Ссылки в 5.2.2.1 и 5.2.2.2 относятся к измерениям, являющимся или не являющимся дорогостоящими, и должны истолковываться не только с финансовой точки зрения, но и исходя из того, является ли измерение сложным, затруднительным или трудоемким (требующим много времени на выполнение).
5.2.1 Единичный результат измерений
Получение только одного результата измерений не является общепринятым в производственной практике. В этом случае невозможно провести прямую статистическую проверку приемлемости такого результата измерений относительно заданного показателя повторяемости. Если результат измерений может оказаться некорректным, должен быть получен второй результат. Наличие двух результатов измерений является основанием для более распространенной практики, которая будет описана ниже.
5.2.2 Два результата измерений
Два результата измерений должны быть получены в условиях повторяемости. Абсолютное расхождение между ними должно в таком случае сравниваться с пределом повторяемости  .
.
5.2.2.1 Случай, когда получение результатов измерений не является дорогостоящим
Если абсолютное расхождение между результатами двух измерений не превышает r, оба результата признают приемлемыми, и в качестве окончательного результата должно указываться среднее арифметическое значение результатов двух измерений. Если абсолютное расхождение превышает r, лаборатория должна получить еще два результата измерений.
Если при этом диапазон  результатов четырех измерений равен или меньше по значению критического диапазона для уровня вероятности 95% для n = 4,
результатов четырех измерений равен или меньше по значению критического диапазона для уровня вероятности 95% для n = 4,  , то в качестве окончательного результата должно фиксироваться среднее арифметическое значение результатов четырех измерений. Коэффициенты критического диапазона f(n) для интервала от n = 2 до n = 40 и для выбранных значений от n = 45 до n = 100 представлены в таблице 1 и предназначены для использования в расчетах критического диапазона согласно равенству
, то в качестве окончательного результата должно фиксироваться среднее арифметическое значение результатов четырех измерений. Коэффициенты критического диапазона f(n) для интервала от n = 2 до n = 40 и для выбранных значений от n = 45 до n = 100 представлены в таблице 1 и предназначены для использования в расчетах критического диапазона согласно равенству
Если диапазон результатов четырех измерений больше критического диапазона для n = 4, то в качестве окончательного результата должна фиксироваться медиана результатов четырех измерений.
Данная процедура резюмируется в блок-схеме, представленной на рисунке 1.
5.2.2.2 Случай, когда получение результатов измерений является дорогостоящим
Если абсолютное расхождение между результатами двух измерений не превышает r, оба результата признают приемлемыми, и в качестве окончательного результата должно указываться среднее арифметическое значение результатов этих двух измерений. Если абсолютное расхождение превышает r, лаборатория должна получить еще один результат измерений.

|
|
| 2102 × 1508 пикс. Открыть в новом окне | |

|
|
| 2113 × 1430 пикс. Открыть в новом окне | |
Если при этом диапазон  результатов трех измерений равен или меньше критического диапазона для n = 3,
результатов трех измерений равен или меньше критического диапазона для n = 3, 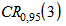 , то в качестве окончательного результата должно фиксироваться среднее арифметическое значение результатов трех измерений.
, то в качестве окончательного результата должно фиксироваться среднее арифметическое значение результатов трех измерений.
Если диапазон результатов трех измерений больше критического диапазона для n = 3, решение принимают в соответствии с нижеследующей альтернативой.
a) Случай, когда невозможно получить четвертый результат измерений
Лаборатория должна использовать в качестве окончательного результата медиану результатов трех измерений.
Данная процедура резюмируется в блок-схеме, представленной на рисунке 2.
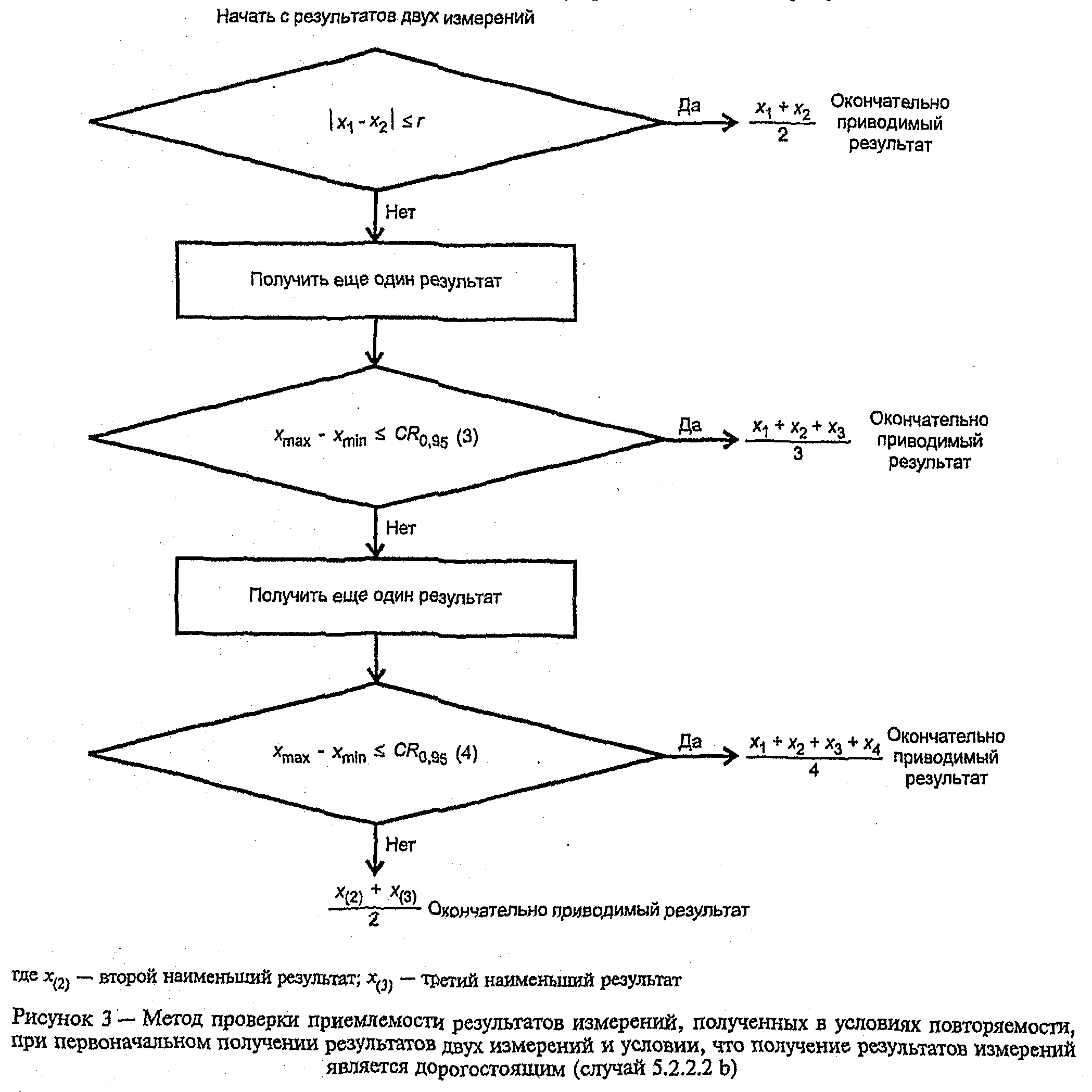
b) Случай, когда возможно получить четвертый результат измерений
Лаборатория должна получить четвертый результат измерений. Если при этом диапазон  результатов четырех измерений равен или меньше критического диапазона для n = 4,
результатов четырех измерений равен или меньше критического диапазона для n = 4,  , то в качестве окончательного результата должно фиксироваться среднее арифметическое значение результатов четырех измерений. Если диапазон результатов четырех измерений больше критического диапазона для n = 4, то в качестве окончательного результата лаборатория должна использовать медиану результатов четырех измерений.
, то в качестве окончательного результата должно фиксироваться среднее арифметическое значение результатов четырех измерений. Если диапазон результатов четырех измерений больше критического диапазона для n = 4, то в качестве окончательного результата лаборатория должна использовать медиану результатов четырех измерений.
Данная процедура резюмируется в блок-схеме, представленной на рисунке 3.
|
|
| 2098 × 2098 пикс. Открыть в новом окне | |
Таблица 1 - Коэффициенты критического диапазона f(n)
n | f(n) | n | f(n) |
2 | 2,8 | 25 | 5,2 |
3 | 3,3 | 26 | 5,2 |
4 | 3,6 | 27 | 5,2 |
5 | 3,9 | 28 | 5,3 |
6 | 4,0 | 29 | 5,3 |
7 | 4,2 | 30 | 5,3 |
8 | 4,3 | 31 | 5,3 |
9 | 4,4 | 32 | 5,3 |
10 | 4,5 | 33 | 5,4 |
11 | 4,6 | 34 | 5,4 |
12 | 4,6 | 35 | 5,4 |
13 | 4,7 | 36 | 5,4 |
14 | 4,7 | 37 | 5,4 |
15 | 4,8 | 38 | 5,5 |
16 | 4,8 | 39 | 5,5 |
17 | 4,9 | 40 | 5,5 |
18 | 4,9 | 45 | 5,6 |
19 | 5,0 | 50 | 5,6 |
20 | 5,0 | 60 | 5,8 |
21 | 5,0 | 70 | 5,9 |
22 | 5,1 | 80 | 5,9 |
23 | 5,1 | 90 | 6,0 |
24 | 5,1 | 100 | 6,1 |
| Примечание - Коэффициент критического диапазона f(n) представляет собой 95%-ный квантиль распределения | |||
5.2.3 Более двух первоначальных результатов измерений
На практике иногда оказывается более двух первоначальных результатов измерений. Метод получения окончательно приводимого результата в условиях повторяемости для случаев, где n > 2, подобен методу для n = 2.
Диапазон  результатов измерений сопоставляют с критическим диапазоном
результатов измерений сопоставляют с критическим диапазоном  , рассчитанным по данным таблицы 1 для соответствующего значения n. Если диапазон результатов не превышает критический, то среднее арифметическое значение результатов всех n измерений используют в качестве окончательного результата.
, рассчитанным по данным таблицы 1 для соответствующего значения n. Если диапазон результатов не превышает критический, то среднее арифметическое значение результатов всех n измерений используют в качестве окончательного результата.
Если диапазон результатов превышает критический диапазон  , то для получения окончательного результата должно быть принято решение в соответствии с одним из вариантов А, В или С, представленных на рисунках 4-6.
, то для получения окончательного результата должно быть принято решение в соответствии с одним из вариантов А, В или С, представленных на рисунках 4-6.
 ar-net.ru
ar-net.ru