СП 16.13330.2017 Стальные конструкции Актуализированная редакция СНиПII-23-81 стр. 38

826 × 469 пикс.     Открыть в новом окне

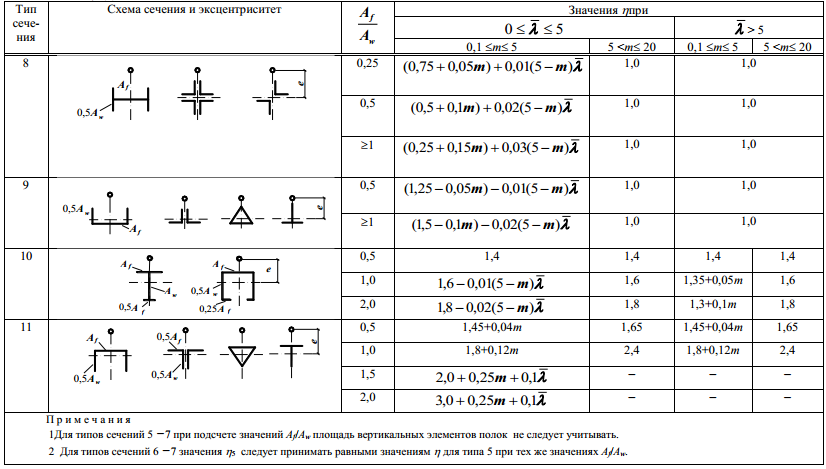
Т а б л и ц а Д.3 – Коэффициенты устойчивости fе при внецентренном сжатиисплошностенчатых стержней в плоскости действия момента, совпадающей с плоскостью симметрии

Условная Гибкость	Значение fе при приведенном относительном эксцентриситете mef
	0,1	0,25	0,5	0,75	1,0	1,25	1,5	1,75	2,0
0,5	967	922	850	782	722	669	620	577	538
1,0	925	854	778	711	653	600	563	520	484
1,5	875	804	716	647	593	548	507	470	439
2,0	813	742	653	587	536	496	457	425	397
2,5	742	672	587	526	480	442	410	383	357
3,0	667	597	520	465	425	395	365	342	320
3,5	587	522	455	408	375	350	325	303	287
4,0	505	447	394	356	330	309	289	270	256
4,5	418	382	342	310	288	272	257	242	229
5,0	354	326	295	273	253	239	225	215	205
5,5	302	280	256	240	224	212	200	192	184
6,0	258	244	223	210	198	190	178	172	166
6,5	223	213	196	185	176	170	160	155	149
7,0	194	186	173	163	157	152	145	141	136
8,0	152	146	138	133	128	121	117	115	113
9,0	122	117	112	107	103	100	098	096	093

Условная Гибкость	Значение fе при приведенном относительном эксцентриситете mef
	2,5	3,0	3,5	4,0	4,5	5,0	5,5	6,0	6,5
0,5	469	417	370	337	307	280	260	237	222
1,0	427	382	341	307	283	259	240	225	209
1,5	388	347	312	283	262	240	223	207	195
2,0	352	315	286	260	240	222	206	193	182
2,5	317	287	262	238	220	204	190	178	168
3,0	287	260	238	217	202	187	175	166	156
3,5	258	233	216	198	183	172	162	153	145
4,0	232	212	197	181	168	158	149	140	135
4,5	208	192	178	165	155	146	137	130	125
5,0	188	175	162	150	143	135	126	120	117
5,5	170	158	148	138	132	124	117	112	108
6,0	153	145	137	128	120	115	109	104	100
6,5	140	132	125	117	112	106	101	097	094
7,0	127	121	115	108	102	098	094	091	087
8,0	106	100	095	091	087	083	081	078	076

Окончание таблицы Д.3

Условная Гибкость	Значение fе при приведенном относительном эксцентриситете mef
	7,0	8,0	9,0	10	12	14	17	20
0,5	210	183	164	150	125	106	090	077
1,0	196	175	157	142	121	103	086	074
1,5	182	163	148	134	114	099	082	070
2,0	170	153	138	125	107	094	079	067
2,5	158	144	130	118	101	090	076	065
3,0	147	135	123	112	097	086	073	063
3,5	137	125	115	106	092	082	069	060
4,0	127	118	108	098	088	078	066	057
4,5	118	110	101	093	083	075	064	055
5,0	111	103	095	088	079	072	062	053
5,5	104	095	089	084	075	069	060	051
П р и м е ч а н и я 1Значения коэффициентов fе в таблице увеличены в 1000 раз. 2Значения fе следует принимать не более значений f.

Т а б л и ц а Д.4 – Коэффициенты устойчивости fе при внецентренном сжатии сквозныхстержней в плоскости действия момента, совпадающей с плоскостьюсимметрии

Условная приведенная гибкость	Значение fе при относительном эксцентриситете m
	0,1	0,25	0,5	0,75	1,0	1,25	1,5	1,75	2,0
0,5	908	800	666	571	500	444	400	364	333
1,0	872	762	640	553	483	431	387	351	328
1,5	830	727	600	517	454	407	367	336	311
2,0	774	673	556	479	423	381	346	318	293
2,5	708	608	507	439	391	354	322	297	274
3,0	637	545	455	399	356	324	296	275	255
3,5	562	480	402	355	320	294	270	251	235
4,0	484	422	357	317	288	264	246	228	215
4,5	415	365	315	281	258	237	223	207	196
5,0	350	315	277	250	230	212	201	186	178
5,5	300	273	245	223	203	192	182	172	163
6,0	255	237	216	198	183	174	165	156	149
6,5	221	208	190	178	165	157	149	142	137
7,0	192	184	168	160	150	141	135	130	125
8,0	148	142	136	130	123	118	113	108	105

Условная приведенная гибкость	Значение fе при относительном эксцентриситете m
	2,5	3,0	3,5	4,0	4,5	5,0	5,5	6,0	6,5
0,5	286	250	222	200	182	167	154	143	133
1,0	280	243	218	197	180	165	151	142	131
1,5	271	240	211	190	178	163	149	137	128
2,0	255	228	202	183	170	156	143	132	125
2,5	238	215	192	175	162	148	136	127	120
3,0	222	201	182	165	153	138	130	121	116
3,5	206	187	170	155	143	130	123	115	110
4,0	191	173	160	145	133	124	118	110	105
4,5	176	160	149	136	124	116	110	105	096
5,0	161	149	138	127	117	108	104	100	095

Условная приведенная гибкость	Значение fе при относительном эксцентриситете m
	7,0	8,0	9,0	10	12	14	17	20
0,5	125	111	100	091	077	067	058	048
1,0	121	109	098	090	077	066	055	046
1,5	119	108	096	088	077	065	053	045
2,0	117	106	095	086	076	064	052	045
2,5	113	103	093	083	074	062	051	044
3,0	110	100	091	081	071	061	051	043
3,5	106	096	088	078	069	059	050	042
4,0	100	093	084	076	067	057	049	041
4,5	096	089	079	073	065	055	048	040
П р и м е ч а н и я 1 Значения коэффициентов fе в таблице увеличены в 1000 раз. 2 Значения fе следует принимать не более значений f.

Т а б л и ц а Д.5 –Приведенные относительные эксцентриситеты mef для внецентренно сжатых стержней с шарнирно опёртыми концами

597 × 699 пикс.     Открыть в новом окне

1. Коэффициент cmax для сечений типов1, 2, 3, приведенных на рисунках в таблице Д.6,следует вычислять по формуле

235 × 75 пикс.     Открыть в новом окне

(Д.1) где (Д.2)

a= ax/h – отношение расстояния ах между центром тяжести и центром изгиба сечения к высоте сечения h;

ех = Mx/N– эксцентриситет приложения сжимающей силы относительно оси х - х, принимаемый со своим знаком (в таблице Д.6 приведен со знаком «плюс»);

А – площадь сечения.

r= (Ix+Iy) / (Ah²) + a ²;

o= I_o /(Iyh²)– здесь I_o - cекториальный момент инерции сечения;

It = (k/3)Sbiti³ – момент инерции сечения при свободном кручении,

bi и ti –ширина и толщина листов соответственно, образующих сечение, включая стенку; k= 1,29– для двутаврового сечения с двумя осями симметрии; k= 1,25– для двутаврового сечения с одной осью симметрии; k=1,20 – для таврового сечения, k= 1,12– для швеллерного (П-образного) сечения.

2 Коэффициент cmax при расчёте на устойчивость стержня П-образного сечения на центральное сжатие (тип 4 при обозначениях, принятых в таблице Д.6,и Iу>Iх) следует вычислять по формуле (Д.1) при ех = 0 и v =0 (тогда В = 1), учитывая при этом, что

А= h tf(2 + i);

Io = tf h³b² (3 +2i) / [12 (6 + i)] = А h²b² (3 +2 i) / [12 (6 + i)(2 + i)];

Iy = h tf b² (6 + i) / 12 = A b² (6 + i) / [12 (2 + i)];

Ix = tf h³ (1 +2i) / [3 (2 +i)] = Ah² (1 +2i) / [3 (2 +i)²].

3 Коэффициент cmax при расчёте на устойчивость стержня швеллерного сечения (тип 5 при обозначениях, принятых в таблице Д.6, и Iх>Iу ), следует вычислять по формуле 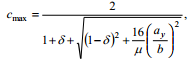(Д.3)

(Д.3)

где d = 4r/µ;

m= 8o + 0,156It lх²/(Аb²) + a ²;

a= ay/b –отношение расстояния ау между центром тяжести и центром изгиба сечения к ширине сечения b – см. таблицу Д.6;

ay = 4 i1b(3i1 +1)/ [(2i1+ 1) (6i1 +1)];

r= (Ix+Iy) / (Ab²) + a²;

It = 0,37 Sbiti³ ; bi и ti – соответственно ширина и толщина листов, образующих сечение;

o= Io / (Ixb²) – см. таблицу Д.6.

При этом:

A = htw(2i1+ 1);

Io = i1twh³b² (3i1 +2) / [12 (6i1 +1)];

Iy = 2i1tw hb²b² ( i1² + 2,5i1+ 1) / (2i1+ 1)²;

Ix= twh³ (6i1 +1) / 12.

Формулы для определения o, a и v или их значения приведены в таблице Д.6.

Т а б л и ц а Д.6 – Коэффициенты, o, a и v

555 × 756 пикс.     Открыть в новом окне