Свод правил СП 16.13330.2017 "Стальные конструкции" Актуализированная редакция СНиП II-23-81* (утв. приказом Министерства строительства и жилищно-коммунального хозяйства РФ от 27 февраля 2017 г. N 126/пр) стр. 13

где х, у - расстояния от главных осей до рассматриваемой точки сечения.

9.1.2 Расчёт на прочность внецентренно сжатых (сжато-изгибаемых) элементов по формуле (105) выполнять не требуется при значении приведенного относительного эксцентриситета (9.2.2), отсутствии ослабления сечения и одинаковых значениях изгибающих моментов, принимаемых в расчетах на прочность и устойчивость.

9.1.3 Внецентренно сжатые (сжато-изгибаемые) элементы из стали с нормативным сопротивлением , с несимметричными сечениями относительно оси, перпендикулярной к плоскости изгиба (например, сечения типов 10, 11 по таблице Д.2), следует проверять на прочность растянутого волокна сечения в плоскости действия момента по формуле

, (107)

где - момент сопротивления сечения, вычисленный для растянутого волокна;

- коэффициент, определяемый по формуле

. (108)

9.2 Расчёт на устойчивость элементов сплошного сечения

9.2.1 Расчёт на устойчивость внецентренно сжатых (сжато-изгибаемых) элементов при действии момента в одной из главных плоскостей следует выполнять как в этой плоскости (плоская форма потери устойчивости), так и из этой плоскости (изгибно-крутильная форма потери устойчивости).

9.2.2 Расчёт на устойчивость внецентренно сжатых (сжато-изгибаемых) элементов постоянного сечения (колонн многоэтажных зданий - в пределах этажа) в плоскости действия момента, совпадающей с плоскостью симметрии, следует выполнять по формуле

. (109)

В формуле (109) коэффициент устойчивости при сжатии с изгибом следует определять по таблице Д.3 в зависимости от условной гибкости и приведенного относительного эксцентриситета , определяемого по формуле

, (110)

где - коэффициент влияния формы сечения, определяемый по таблице Д.2 (приложение Д);

- относительный эксцентриситет (здесь е = М / N - эксцентриситет, при вычислении которого значения М и N следует принимать согласно требованиям 9.2.3;

- момент сопротивления сечения, вычисленный для наиболее сжатого волокна).

При значениях расчет следует выполнять как для изгибаемых элементов (раздел 8).

9.2.3 Расчётные значения продольной силы N и изгибающего момента М в элементе следует принимать для одного и того же сочетания нагрузок из расчёта системы по недеформированной схеме в предположении упругих деформаций стали.

При этом значения М следует принимать равными:

для колонны постоянного сечения рамной системы - наибольшему моменту в пределах длины колонны;

для ступенчатой колонны - наибольшему моменту на длине участка постоянного сечения;

для колонны с одним защемлённым, а другим свободным концом - моменту в заделке, но не менее момента в сечении, отстоящем на треть длины колонны от заделки;

для сжатых поясов ферм и структурных плит, воспринимающих внеузловую поперечную нагрузку, - наибольшему моменту в пределах средней трети длины панели пояса, определяемому из расчёта пояса как упругой неразрезной балки;

для сжатого стержня с шарнирно-опёртыми концами и сечением, имеющим одну ось симметрии, совпадающую с плоскостью изгиба, - моменту, определяемому по формулам таблицы 20 в зависимости от относительного эксцентриситета и принимаемому равным не менее .

Таблица 20

Относительный эксцентриситет	Момент М при условной гибкости стержня
Обозначения, принятые в таблице 20: - наибольший изгибающий момент в пределах длины стержня; - наибольший изгибающий момент в пределах средней трети длины стержня, принимаемый равным не менее ; - изгибающий момент, принимаемый равным М при и , но не менее .

Для сжатых стержней двоякосимметричного сплошного сечения с шарнирно-опёртыми концами, на которых действуют изгибающие моменты, значение , необходимое для определения , следует принимать согласно таблице Д.5 (приложение Д).

9.2.4 Расчёт на устойчивость внецентренно сжатых (сжато-изгибаемых) стержней сплошного постоянного сечения, кроме коробчатого, из плоскости действия момента при изгибе их в плоскости наибольшей жёсткости , совпадающей с плоскостью симметрии, а также швеллеров следует выполнять по формуле

, (111)

где с - коэффициент, определяемый согласно требованиям 9.2.5;

- коэффициент устойчивости при центральном сжатии, определяемый согласно требованиям 7.1.3.

9.2.5 Коэффициент с в формуле (111) следует определять:

при значениях по формуле

, (112)

где , - коэффициенты, определяемые по таблице 21;

при значениях по формуле

, (113)

где - коэффициент устойчивости при изгибе, определяемый согласно требованиям 8.4.1 и приложению Ж как для балки с двумя и более закреплениями сжатого пояса;

при значениях по формуле

207 × 27 пикс.     Открыть в новом окне

, (114)

где следует определять: - по формуле (112) при ; - по формуле (113) при . Здесь - относительный эксцентриситет, где следует принимать по 9.2.6.

При гибкости коэффициент с не должен превышать значений , определяемых по приложению Д; в случае, если , в формулах (111) и (117) вместо с следует принимать .

При значениях отношения ширины сечения к его высоте менее 0,3 коэффициент с следует принимать, равным 0,3.

Таблица 21

Тип сечения	Схема сечения и эксцентриситет	Значения коэффициентов
		при		при
1	200 × 147 пикс.     Открыть в новом окне	0,7		1
2	252 × 140 пикс.     Открыть в новом окне
3	175 × 163 пикс.     Открыть в новом окне
4	254 × 134 пикс.     Открыть в новом окне			1	; при
Обозначения, принятые в таблице 21: и - моменты инерции большей и меньшей полок относительно оси симметрии сечения у-у соответственно; - значение при .

9.2.6 При определении относительного эксцентриситета в формулах (112) - (114) за расчётный момент следует принимать:

для стержней с концами, закрепленными от смещения перпендикулярно плоскости действия момента, - максимальный момент в пределах средней трети длины, но не менее половины наибольшего момента по длине стержня;

для стержней с одним защемленным, а другим свободным концом - момент в заделке, но не менее момента в сечении, отстоящем на треть длины стержня от заделки.

9.2.7 Расчёт на устойчивость внецентренно сжатых (сжато-изгибаемых) элементов двутаврового сечения, непрерывно подкрепленных вдоль одной из полок, следует выполнять по приложению Ж.

9.2.8 Внецентренно сжатые (сжато-изгибаемые) элементы постоянного сечения, изгибаемые в плоскости наименьшей жесткости ( и ), следует рассчитывать по формуле (109), а при гибкости 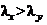- также проверять расчётом на устойчивость из плоскости действия момента как центрально сжатые элементы по формуле