Остальные обозначения – см. формулы (6.7) и (6.8).
Суммирование в знаменателе формулы (6.12) распространяется на все проемы.
6.3.16 Горизонтальные несущие подсистемы – диски перекрытий в многоэтажных зданиях, наряду с восприятием полезной нагрузки и передачей ее на вертикальные элементы, деформируясь в своей плоскости выполняют роль горизонтальных диафрагм, связывающих вертикальные несущие конструкции в единую пространственную систему, перераспределяя между ними внешние нагрузки.
Из-за податливости многочисленных швов жесткость дисков перекрытия и покрытия существенно снижается по сравнению со сплошным монолитным перекрытием. Снижение допускается учитывать введением пониженного значения модуля упругости при постоянном соотношении между приведенными модулями сдвига и упругости, принимаемом для сборных перекрытий при качественной заделке швов в соответствии с 6.2.4.
6.3.17 При определении жесткости дисков перекрытий из сборных железобетонных плит по сборным ригелям в своей плоскости следует учитывать податливость, вызванную за счет повышенной деформативности соединений на опорах и межплитных швов (рисунок 6.5).
 | |
| 991 × 607 пикс. Открыть в новом окне | |
Рисунок 6.5 – Фрагмент сборного перекрытия из многопустотных плит
6.3.18 В сборных перекрытиях применяются следующие типы стыков:
- вертикальные стыки торцов плит через бетонные швы с опорными конструкциями – ригелями;
- продольные стыки между плитами;
-горизонтальные стыки (швы) плит по опорным площадкам с поддерживающими конструкциями (стенами, балками или ригелями).
Совместная работа многопустотных плит обеспечивается замоноличенными швами и сварными соединениями (для связевых и пристенных плит). Для увеличения сцепления бетона швов с конструкциями на их боковой поверхности устраиваются углубления для образования шпонок.
6.3.19 При моделировании взаимодействия рядовых многопустотных плит с поддерживающими конструкциями (ригели, балки и несущие стены) при горизонтальных нагрузках следует учитывать силы трения и сцепления подстилающего растворного слоя по опорным площадкам.
Торцевые швы между плитами и поддерживающими конструкциями работают только на сжатие и сдвиг перпендикулярно к пролету плит.
6.3.20 Взаимодействие ребристых плит с ригелями и балками при горизонтальных нагрузках следует обеспечивать сварными соединениями опорных закладных деталей. Совместная работа плит при вертикальных нагрузках обеспечивается продольными бетонными швами, выполняемыми, как правило, со шпонками.
6.3.21 Расчетные схемы сборных балочных дисков перекрытий для расчета на горизонтальные нагрузки, фрагмент которой показан на рисунке 6.6, зависят в основном от типа плиты перекрытия, конструкции продольных швов и условий опирания.
Концентрация деформаций происходит в зонах сопряжений сборных конструкций, на основании этого расчетную модель ячейки перекрытия рекомендуется представлять в виде (рисунок 6.6) плоскостных 1 и стержневых 2 элементов, соединенных деформируемыми связями 3. Учет работы перекрытия из своей плоскости производится путем применения в расчетной модели пластин и связей как пространственных элементов.
 | |
| 669 × 402 пикс. Открыть в новом окне | |
а– расчетная модель ячейки перекрытия; б – схемы деформирования при наличии связей
Рисунок 6.6 – Расчетная модель ячейки перекрытия и схемы деформирования
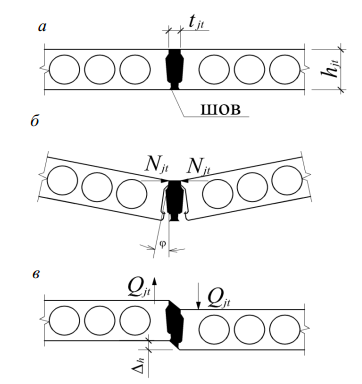
6.3.22 Жесткость бетонного межплитного шва на изгиб следует принимать равной нулю, то есть шов рассматривается как цилиндрический шарнир. Однако сжимающая шов сила прикладывается не по оси боковой грани плит (рисунок 6.7) – возникает внецентренное сжатие. Поэтому цилиндрический шарнир следует располагать по оси действия сжимающего усилия или в уровне сжатой грани плиты.
 | |
| 362 × 384 пикс. Открыть в новом окне | |
а– схема межплитного шва; б – поворот вдоль продольной оси; в – сдвиг плит
Рисунок 6.7 – Схема работы продольного межплитного шва
6.3.23 Жесткость межплитного шва на сдвиг равна соответствующему усилию Qjt, вызывающему единичные перемещения ?h, определяемому по формуле
Dsh = Qjt / ?h. (6.15)
Для участка шва, толщиной tjt, высотой hjt и длиной вдоль оси плиты ljt:
 | |
| 234 × 61 пикс. Открыть в новом окне | |
где n = 1,2 – коэффициент, учитывающий неравномерность касательных напряжений по площади поперечного сечения элемента.
Влияние сдвиговой жесткости шва на совместную работу плит следует учитывать для Dsh=300 кН/м, что существенно меньше реальной жесткости. Для швов между типовыми многопустотными плитами значение сдвиговой жесткости Сsh на 1 м шва составляет 308 ? 105 кН/м.
6.3.24 Растягивающие усилия в плоскости диска перекрытия из многопустотных плит воспринимаются в одном направлении связевыми межколонными плитами, в другом – ригелями.
Линейную податливость связевых плит следует определять, согласно схеме на рисунке 6.8 по формуле
 | |
| 340 × 58 пикс. Открыть в новом окне | |
 | |
| 1337 × 481 пикс. Открыть в новом окне | |
1 – плиты; 2 – ригели; 3 – колонны; 4 – арматурные связи
Рисунок 6.8 – Расчетная схема к определению жесткости связевой плиты при растяжении в плоскости диска перекрытия
6.3.25 Жесткость на растяжение по зоне опирания связевой многопустотной или сплошной плиты на ригель (балку) следует определять по формуле
 | |
| 255 × 65 пикс. Открыть в новом окне | |
где Ns = As ss – усилие в связевой арматуре;
Nsup = Asup ssup ftr – усилие для преодоления трения по площадкам опирания плит на поддерживающие конструкции;
здесь Asup и ssup – площадь опирания и опорное давление плиты на ригель;
ftr – коэффициент трения плиты об опорную конструкцию;
?z – деформации закладной детали, определяемые по расчету и принимаемые не более 2 мм.
6.3.26 Жесткость трения пустотной плиты рекомендуется определять при деформациях сдвига равных esd =100 ? 10-5.
6.3.27 В перекрытиях из ребристых плит при воздействии горизонтальной нагрузки на перекрытие опорное соединение воспринимает сдвигающее усилие, изгиб и кручение в своей плоскости. Суммарные линейные перемещения в сопряжении в общем случае следует определять сложением деформаций закладных деталей ригеля (?xr) и ребра (?xp) плиты
?xzi =?xr+?xp (6.19)
Опорное сопряжение ребристой плиты с ригелем рекомендуется представлять в виде стержня, сечение и длина которого определяется из условия равенства линейных и угловых деформаций.
Жесткость элемента связи при растяжении-сжатии в этом случае определяется по формуле
 ar-net.ru
ar-net.ru