0.2 Необходимость рассмотрения "прецизионности" возникает из-за того, что измерения, выполняемые на предположительно идентичных материалах при предположительно идентичных обстоятельствах, не дают, как правило, идентичных результатов. Это объясняется неизбежными случайными погрешностями, присущими каждой измерительной процедуре; факторы, оказывающие влияние на результат измерения, не поддаются полному контролю. При практической интерпретации данных измерений эта изменчивость должна учитываться. Например, нельзя установить фактическое отклонение полученного результата измерений от некоторого определенного значения измеряемой величины, если он лежит в области неизбежных случайных погрешностей измерительной процедуры. Аналогичным образом, сопоставление результатов измерений измеряемых характеристик двух партий материала не выявит какого-либо существенного различия в качестве, если расхождение между результатами лежит в вышеупомянутой области.
0.3 В частях 1-5 ИСО 5725 обсуждаются подходы и приводятся методы оценки прецизионности (выраженной через стандартные отклонения повторяемости и воспроизводимости) и правильности (выраженной через различные составляющие систематической погрешности) измерений, выполняемых стандартным методом. Такая оценка, однако, была бы бесцельной, если бы ее результаты нельзя было использовать на практике.
0.4 Исходя из того, что точность метода измерений установлена, в настоящей части ИСО 5725 даны области применения значений точности на практике, например, в области продвижения коммерческих сделок или контроля показателей работы лабораторий и признания их технической компетентности.
1 Область применения
1.1 Цель настоящего стандарта - дать общее представление о некоторых способах использования данных о точности в различных практических ситуациях, а именно:
a) представить стандартный метод расчета пределов повторяемости (сходимости), воспроизводимости и других пределов, используемых при рассмотрении результатов измерений, полученных при реализации стандартного метода измерений;
b) обеспечить способы проверки приемлемости результатов измерений, полученных в условиях повторяемости или воспроизводимости;
с) описать способ оценки стабильности результатов, получаемых в пределах одной лаборатории за определенный период времени, и таким образом внедрить метод "контроля качества" операций в пределах этой лаборатории;
d) описать подходы к оценке способности данной лаборатории правильно применять (реализовывать) данный стандартный метод измерений;
e) описать способы сопоставления альтернативных методов измерений.
1.2 Настоящий стандарт относится исключительно к методам измерений непрерывных (в смысле принимаемых значений в измеряемом диапазоне) величин, дающим в качестве результата измерений единственное значение. При этом единственное значение может быть и результатом расчета, основанного на ряде измерений одной и той же величины.
1.3 Предполагается, что оценки правильности и прецизионности были получены в соответствии с ГОСТ Р ИСО 5725-1 - ГОСТ Р ИСО 5725-5.
1.4 Дополнительная информация, относящаяся к сфере применения значений точности на практике, будет представляться в начале каждого раздела.
2 Нормативные ссылки
В настоящем стандарте использованы ссылки на следующие стандарты:
ГОСТ 8.315-97 Государственная система обеспечения единства измерений. Стандартные образцы состава и свойств веществ и материалов. Основные положения
ГОСТ Р ИСО 5725-1-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 1. Основные положения и определения
ГОСТ Р ИСО 5725-2-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 2. Основной метод определения повторяемости и воспроизводимости стандартного метода измерений
ГОСТ Р ИСО 5725-3-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 3. Промежуточные показатели прецизионности стандартного метода измерений
ГОСТ Р ИСО 5725-4-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 4. Основные методы определения правильности стандартного метода измерений
ГОСТ Р ИСО 5725-5-2002 Точность (правильность и прецизионность) методов и результатов измерений. Часть 5. Альтернативные методы определения прецизионности стандартного метода измерений
ГОСТ Р 50779.42-99 (ИСО 8258-91) Статистические методы. Контрольные карты Шухарта
3 Определения
В настоящем стандарте применяют термины с определениями, представленные в ИСО 3534-1 [1] и ГОСТ Р ИСО 5725-1.
Условные обозначения, используемые в ГОСТ Р ИСО 5725, приведены в приложении А.
4 Нахождение пределов
4.1 Пределы повторяемости и воспроизводимости
4.1.1 В ГОСТ Р ИСО 5725-2 основное внимание было сосредоточено на оценке стандартных отклонений при работе в условиях повторяемости или воспроизводимости. Однако в обычной лабораторной практике требуется рассмотрение различий между двумя или большим числом результатов измерений, и для этого требуется некая мера, близкая скорее к критическому различию, чем к стандартному отклонению.
4.1.2 Мера, основывающаяся на суммах или разностях из n независимых случайных величин, каждая из которых характеризуется стандартным отклонением 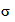 , будет иметь стандартное отклонение
, будет иметь стандартное отклонение  . Предел воспроизводимости (R) или предел повторяемости (r) - расхождения между двумя результатами измерений; для них стандартное отклонение составит
. Предел воспроизводимости (R) или предел повторяемости (r) - расхождения между двумя результатами измерений; для них стандартное отклонение составит  .
.
Обычно в статистике для рассмотрения различия между этими двумя случайными величинами используют множитель f перед стандартным отклонением, то есть  . Величина f (называемая коэффициентом критического диапазона) зависит от доверительного уровня вероятности и закона распределения случайной величины. Для пределов воспроизводимости и повторяемости доверительный уровень вероятности составляет 95%, и в ГОСТ Р ИСО 5725 делается допущение, что лежащее в основе распределение является приближенно нормальным. Для нормального распределения на уровне вероятности 95% коэффициент f равен 1,96, и
. Величина f (называемая коэффициентом критического диапазона) зависит от доверительного уровня вероятности и закона распределения случайной величины. Для пределов воспроизводимости и повторяемости доверительный уровень вероятности составляет 95%, и в ГОСТ Р ИСО 5725 делается допущение, что лежащее в основе распределение является приближенно нормальным. Для нормального распределения на уровне вероятности 95% коэффициент f равен 1,96, и  тогда равен 2,77.
тогда равен 2,77.
Поскольку цель настоящего стандарта - дать несколько простых правил для применения не статистиками при рассмотрении результатов измерений, представляется целесообразным использовать округленное значение 2,8 вместо  .
.
4.1.3 Процедура оценки прецизионности основывается на оценке истинных стандартных отклонений, в то время как сами истинные стандартные отклонения остаются неизвестными. Следовательно, в статистической практике они должны быть обозначены скорее через s, чем через  . Однако, если при этом предусматривается использование процедур, данных в ГОСТ Р ИСО 5725-1 и ГОСТ Р ИСО 5725-2, то эти оценки будут основываться на существенном количестве результатов измерений и дадут наилучшую информацию, которую можно иметь об истинных значениях стандартных отклонений. В других рассматриваемых ниже случаях для оценок стандартных отклонений, основанных на более ограниченных данных, используют символ s (оценка стандартного отклонения). Таким образом, лучше использовать символ
. Однако, если при этом предусматривается использование процедур, данных в ГОСТ Р ИСО 5725-1 и ГОСТ Р ИСО 5725-2, то эти оценки будут основываться на существенном количестве результатов измерений и дадут наилучшую информацию, которую можно иметь об истинных значениях стандартных отклонений. В других рассматриваемых ниже случаях для оценок стандартных отклонений, основанных на более ограниченных данных, используют символ s (оценка стандартного отклонения). Таким образом, лучше использовать символ  для обозначения значений, полученных из полного эксперимента по оценке прецизионности, и воспринимать его как истинное стандартное отклонение, с которым будут сопоставляться другие оценки (s).
для обозначения значений, полученных из полного эксперимента по оценке прецизионности, и воспринимать его как истинное стандартное отклонение, с которым будут сопоставляться другие оценки (s).
4.1.4 Исходя из 4.1.1 - 4.1.3, сопоставление разностей двух результатов измерений, полученных в условиях повторяемости или воспроизводимости, должно осуществляться с пределом повторяемости 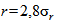 или с пределом воспроизводимости
или с пределом воспроизводимости  .
.
4.2 Сопоставления на основании произвольного количества значений (более двух)
4.2.1 Две группы измерений в одной лаборатории
Если в одной лаборатории в условиях повторяемости выполнено две группы измерений: первая группа, давшая  результатов измерений со средним арифметическим значением
результатов измерений со средним арифметическим значением 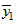 , и вторая группа, давшая
, и вторая группа, давшая  результатов измерений со средним арифметическим значением
результатов измерений со средним арифметическим значением 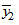 , - то стандартное отклонение разности
, - то стандартное отклонение разности 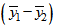 составит
составит
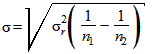 ,
,
и критическая разность для 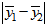 будет выглядеть следующим образом
будет выглядеть следующим образом
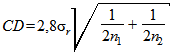
на уровне вероятности 95%.
Примечание 1 - Если 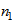 и
и 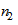 равны единице, то, как и должно быть, получим
равны единице, то, как и должно быть, получим 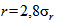 .
.
4.2.2 Две группы измерений в двух лабораториях
Если первая из лабораторий получает  результатов измерений со средним арифметическим значением
результатов измерений со средним арифметическим значением  , а вторая -
, а вторая -  результатов измерений со средним арифметическим значением
результатов измерений со средним арифметическим значением  , причем в каждом случае - в условиях повторяемости, то стандартное отклонение разности
, причем в каждом случае - в условиях повторяемости, то стандартное отклонение разности  составит:
составит:
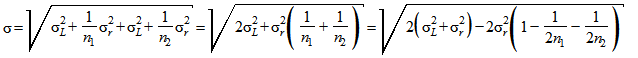
|
|
| 638 × 58 пикс. Открыть в новом окне | |
и критическая разность для  будет выглядеть следующим образом:
будет выглядеть следующим образом:

|
|
| 317 × 58 пикс. Открыть в новом окне | |
на уровне вероятности 95%.
Примечание 2 - Если  и
и 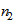 равны единице, то, как и должно быть, получим
равны единице, то, как и должно быть, получим  .
.
4.2.3 Сопоставление с опорным значением для одной лаборатории
Если в пределах одной лаборатории в условиях повторяемости получено n результатов измерений со средним арифметическим значением  , затем выполнено сопоставление с данным опорным значением
, затем выполнено сопоставление с данным опорным значением 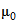 , то в отсутствие конкретных данных по лабораторной составляющей систематической погрешности стандартное отклонение интересующей нас разности
, то в отсутствие конкретных данных по лабораторной составляющей систематической погрешности стандартное отклонение интересующей нас разности 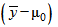 (где
(где 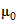 - принятое опорное значение) равно
- принятое опорное значение) равно
 ar-net.ru
ar-net.ru